Практико-ориентированные задачи как средство развития математической грамотности в 5-6 классах
Одним из ресурсов повышения качества современного школьного математического образования является формирование функциональной грамотности учащихся. Формирование функциональной грамотности учащихся считается важнейшим требованием реализации ФГОС.
Функциональная грамотность понимается в современной дидактике как способность человека использовать постоянно приобретаемые в течение жизни знания, умения и навыки для решения максимально широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений.
Функциональная грамотность включает математическую грамотность, оценивание которой положено в основу проверки математической подготовки в рамках исследования PISA. Математическая грамотность трактуется как способность индивидуума проводить математические рассуждения, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира.
Важнейшей составляющей математической грамотности является умение использовать имеющиеся предметные знания при решении задач, приближённых к реальным ситуациям, так называемых практико-ориентированных задач по математике.
Практико-ориентированная математическая задача понимается нами как задача, фабула которой раскрывает приложения математики в смежных учебных дисциплинах, знакомит с ее использованием в быту, в сфере обслуживания, в экономике современного производства.
Значение решения практико-ориентированных задач по математике определяется следующими факторами:
– повышение мотивации учеников к математическим задачам с практико-ориентированным сюжетом;
– более осмысленное решение задачи;
– развитие ассоциативного и логического мышления;
– формирование у учащихся умения описывать реальные жизненные ситуации математическим языком;
– осознание учащимися важности математики как науки, приносящей реальную пользу в повседневной жизни.
Формирование умения выполнять сложные задания по математике, способствующие развитию функциональной грамотности, нужно, конечно, начинать с решения простых практико-ориентированных задач в 5-6 классах, в том числе и по материалу «Делимость, свойства и признаки делимости».
С учётом того, что в учебниках 5-6 класса очень мало практико-ориентированных задач на свойства и признаки делимости, приведём примеры таких задач разного уровня сложности, причём, более сложные – с решением.
Задачи на признак делимости на 2:
Задача № 1. Петя и Коля решили купить футбольный мяч и разделить его стоимость между собой поровну. Смогут ли они разделить стоимость покупки поровну в рублях, если мяч стоит 665 рублей?
Задача № 2. В школу привезли новые стулья. Мальчики помогли перенести их в кабинеты, беря по 2 стула каждый раз. Сколько стульев могли привезти в школу?
А) 108; Б) 115; В): 103; Г) нет верного ответа.
Задачи на признак делимости на 3:
Задача № 3. Собранную свеклу заложили в 3 овощехранилища. Может ли быть, что собрано 147 т. свеклы? 352 т. свеклы?
Задача № 4. Фермер собрал 123 кг яблок. Нужно разложить яблоки в мешки для продажи на рынке. Фермер хочет положить такое количество яблок в каждый мешок, чтобы лишних не осталось. Какое количество мешков понадобится?
Задачи на признак делимости на 5:
Задача № 5. В школьную столовую привезли упаковки с коробками сока – по 5 коробок в каждой упаковке. Может ли быть всего 37 коробок сока? 60 коробок сока? 45 коробок сока?
Задача № 6. Мама купила Кате канцелярские принадлежности. Весь товар продавец разложила в пакеты по 5 предметов в каждый. Может ли общее число принадлежностей быть равным
А) 11; Б) 15; В) 16.
Задачи на признак делимости на 9:
Задача № 7. На каждом этаже в доме по 9 квартир. Может ли количество квартир в доме быть равно 142?
Задача № 8. Собрали 2 ц яблок и часть из них разложили в 9 одинаковых ящиков. Могло ли после этого остаться: 60 кг яблок? 56 кг яблок?
Задачи на признак делимости на 10:
Задача № 9. Бабушка купила несколько пачек печенья, по 10 штук в каждой пачке. Возможно ли, что всего печенья 35 штук?
Задача № 10. Даша купила в магазине 10 одинаковых тетрадей. Продавец назвал стоимость покупки – 176 рублей. Прав ли продавец?
Задачи на несколько признаков делимости:
Задача № 11. Садовник хочет посадить 99 кустов малины так, чтобы они росли ровными рядами с одинаковым количеством кустов в каждом. Сколько рядов получится у садовника?
Задача № 12. В школьную библиотеку привезли 81 новую книгу. Библиотекарю нужно расставить их на полки так, чтобы на каждой было одинаковое число книг. Сколько полок займут книги?
Задачи на признаки делимости составных чисел:
Задача № 13. Батальон солдат из 250 человек готовится к параду. Может ли он построиться в шесть одинаковых шеренг?
Решение: Проверим, делится ли число 250 на 6. Для того чтобы число делилось на 6, оно должно делиться на 2 и на 3.
1) 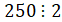 , так как число оканчивается на 0;
, так как число оканчивается на 0;
2) 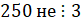 , так как сумма цифр числа не делится на три
, так как сумма цифр числа не делится на три
( 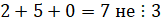 )
)
Значит число 250 не делится на 6, то есть батальон не может построиться в шесть одинаковых шеренг.
Задача № 14. В лекционный зал привезли 120 стульев. Не производя деление, ответьте на вопрос, можно ли их расставить в 15 равных рядов? в 30 рядов? в 45?
Решение:
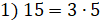 ,
, 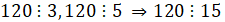 можно расставить;
можно расставить;
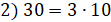 ,
, 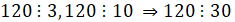 можно расставить;
можно расставить;
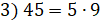 ,
, 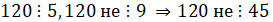 нельзя расставить.
нельзя расставить.
Задачи на свойства и признаки делимости:
Задача № 15. Миша покупает в магазине 4 ручки, 12 тетрадей, 6 блокнотов, 2 стирательные резинки и несколько альбомов для рисования по 78 руб. Продавец пробивает чек на сумму 891 рубль. Посмотрев на чек, мальчик сразу сказал: «Вы ошиблись в подсчете!» Продавец пересчитал и исправил свою ошибку. Как Мише удалось так быстро найти ошибку?
Решение: Количество или стоимость приобретенных товаров каждого вида выражается числом, кратным 2-м. Если каждое из слагаемых делится на 2, то и сумма должна делиться на 2. По признаку делимости на 2: на 2 делятся только те числа, у которых последняя цифра является четной.
Последняя цифра в числе 891 равна 1, которая является нечетной, следовательно, расчет неверен.
Задача № 16. Покупатель взял в магазине пакет молока стоимостью 63 рубля, пачку творога стоимостью 93 рубля, 6 пирожных и 3 килограмма сахара. Когда кассир выбила чек на 487 рублей, покупатель потребовал проверить расчет и исправить ошибку. Как покупатель определил, что счёт неверен?
Решение: Стоимость приобретенных товаров каждого вида выражается числом, кратным 3-м (у молока и творога цена кратна 3-м, цена остальных товаров не известна, но их количество кратно 3-м). Если каждое из слагаемых делится на 3, то и сумма должна делиться на 3. По признаку делимости на 3: на 3 делятся только те числа, сумма цифр которых делится на 3 без остатка.
Сумма цифр числа 487:  на 3 не делится, следовательно, расчет неверен.
на 3 не делится, следовательно, расчет неверен.
Задача № 17. Паше выдали классные деньги в сумме 165 рублей, ему надо было купить для девочек поздравительные открытки к 8 марта. В магазине были открытки по 5 и 10 рублей. Паша решил купить открытки по одинаковой цене на всю сумму без сдачи. Сколько открыток мог купить Паша?
Решение: 165 делится на 5. 165 не делится на 10, следовательно, Паша мог купить без сдачи только:
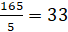 открытки по 5 рублей.
открытки по 5 рублей.
Задача № 18. В июне было подано 27 заявлений о приёме в первый класс, в июле – 33, а в августе – 31. Можно ли из такого количества детей скомплектовать 3 класса с одинаковым количеством учеников?
Решение:
 , а
, а  . Значит общее количество учеников тоже не делится на 3. Поэтому скомплектовать 3 класса с одинаковым количеством учеников нельзя.
. Значит общее количество учеников тоже не делится на 3. Поэтому скомплектовать 3 класса с одинаковым количеством учеников нельзя.
Задача № 19. Для победителей конкурса новогодних костюмов купили 12 шоколадок, 36 конфет и 21 орех. Можно ли собрать 3 одинаковых подарка? 9 одинаковых подарка? 2 одинаковых подарка?
Решение:
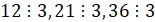 , значит 3 подарка можно собрать.
, значит 3 подарка можно собрать.- 12 не делится на 9, значит 9 подарков собрать нельзя.
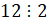 , 21 не делится на 2, значит 2 подарка собрать нельзя.
, 21 не делится на 2, значит 2 подарка собрать нельзя.
Сюжетные практико-ориентированные задачи могут использоваться на уроках для создания проблемной ситуации перед изучением нового материала на свойства и признаки делимости. Одну из таких задач на вполне вероятную жизненную ситуацию учитель может привести при изучении, например, темы «Признак делимости на 3».
Задача № 20. От некоторого финансового документа оторван кусочек, и в результате первая цифра числа a152 неизвестна. Бухгалтер знает, что это число четырехзначное, оно должно делиться на 3 (деньги предстоит разделить на три бригады), а также помнит, что первая цифра этого числа больше 5. Как восстановить неизвестную цифру?
Учащимся предлагается подумать. Так как у них ещё недостаточно знаний для решения данной задачи, учитель может сообщить, что эту цифру можно восстановить с помощью признака делимости на 3. В чем заключается этот признак? Как узнать, делится ли какое-то число на 3, не производя деления?
Далее изучается признак делимости, после чего учитель с классом возвращаются к решению задачи, предложенной в начале урока.
Решение: Так как число должно делиться на 3, то по признаку делимости на 3 первая цифра числа либо 1, либо 4, либо 7. Так как бухгалтер помнит, что первая цифра числа больше 5, то получается, что неизвестная цифра числа равна 7.
Опыт использования приведённых практико-ориентированных задач на уроках и на занятиях математического кружка показал, что их решение способствует мотивации учащихся к изучению математики, а также развитию математической грамотности учащихся.
| Количество просмотров: 4853 |


Добавить комментарий