Развитие функциональной грамотности и нестандартного мышления учащихся на занятиях математического кружка
Развитие функциональной грамотности и нестандартного мышления учащихся – важнейшие задачи современного математического образования. Эти задачи могут и должны решаться не только на уроках, но и во внеурочной работе с учащимися, в частности на занятиях кружка по решению задач повышенной сложности.
Сегодня под функциональной грамотностью понимается способность человека использовать знания, приобретённые навыки для решения самого широкого спектра жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений.
Функциональная грамотность включает математическую грамотность, оценка которой положена в основу проверки математической подготовки в рамках исследования PISA. Математическая грамотность трактуется как способность индивидуума проводить математические рассуждения, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира.
Нестандартное мышление рассматривается нами как мышление, позволяющее учащемуся решать нестандартные задачи, задачи повышенной сложности, олимпиадного уровня.
Для развития математической грамотности и нестандартного мышления учащихся могут использоваться различные способы. Одним из таких способов является решение практико-ориентированных и олимпиадных задач на математическом кружке.
Практико-ориентированная математическая задача понимается нами как задача, фабула которой раскрывает приложения математики в смежных учебных дисциплинах, знакомит с ее использованием в быту, в сфере обслуживания, в экономике современного производства.
Главная идея применения практико-ориентированных задач в обучении математике заключается в организации учебного процесса на основе единства эмоционально-образного и логического компонентов содержания; приобретения новых знаний и формирования практического опыта их использования при решении жизненно важных задач и проблем; эмоционального и познавательно-творческого поиска учащихся.
Рассмотрим примеры практико-ориентированных задач по теме «Свойства и признаки делимости», рассмотрение которых на занятиях математического кружка будет способствовать развитию функциональной грамотности учащихся.
Задача 1. В классе больше 20, но меньше 30 учеников. При этом в классе тех, кто ходит в шахматный кружок, в 2 раза меньше, чем тех, кто не ходит. А тех, кто ходит в шашечный кружок, в 3 раза меньше, чем тех, кто не ходит. Сколько учеников в классе?
Решение: Пусть в шахматный кружок ходит x ребят, тогда в него не ходит 2x ребят. Итак, всего в классе 3x ребят, и количество учеников в классе делится на 3. Аналогично, пусть в шашечный кружок ходит y ребят, тогда в него не ходит 3y ребят. Итак, всего в классе 4y ребят, и количество учеников в классе делится на 4. Число учеников в классе делится и на 3, и на 4, то есть оно делится на 12. Единственное подходящее число, большее 20 и меньшее 30, это 24. Ответ. 24 ученика.
Задача 2. У Пети в 4 карманах лежит несколько монет достоинствами в 2, 5 и 10 рублей. В трёх карманах денег поровну, а в четвёртом – вдвое больше, чем в третьем. Могут ли ровно 7 из Петиных монет быть двухрублёвыми?
Решение: Общая сумма денег у Пети впятеро больше, чем сумма, лежащая в первом кармане, то есть кратна 5. Если бы у него было ровно 7 двухрублёвых монет, общая сумма денег не делилась бы на 5, так как достоинства остальных его монет делятся на 5. Ответ. Не могут.
Задача 3. Фома и Ерема нашли на дороге по пачке 11-рублевок. Фома выпил 3 стакана чая, съел 4 калача и 5 бубликов. Ерема выпил 9 стаканов чая, съел 1 калач и 4 бублика. Стакан чая, калач и бублик стоят по целому числу рублей. Фома может расплатиться 11-рублевками без сдачи. Покажите, что это может сделать и Ерема.
Пусть x руб. стоит стакан чая, y руб. – калач и z руб. – бублик. Тогда Фома потратил на всё 3x + 4y +5z (руб.), по условию эта сумма делится на 11. Ерёма потратил 9x + y + 4z (руб.). Покажем, что эта сумма также делится на 11. Число ЗЗх + 11z очевидно делится на 11, поэтому, если и Зх + 4у + 5z делится на 11, то и их сумма тоже делится на 11, но эта сумма равна 36х + 4у + 16z, т.е. учетверенной сумме, потраченной Еремой, следовательно, и эта сумма делится на 11.
Задача № 4. Туристическое агентство предложило Петру Сидорову тур на Алтай: 2 взрослых путёвки и 1 детскую за 117000 рублей. Известно, детская путёвка на 23000 дешевле взрослой. Каким образом Пётр понял, что его обманывают.
Решение: Если бы детская путёвка не была дешевле взрослой, то Петру пришлось бы заплатить за 3 путёвки
117000 + 23000 = 140000 рублей.
Но 140000 не  3. Поэтому Пётр понял, что его обманывают.
3. Поэтому Пётр понял, что его обманывают.
Задача № 5. В магазине 6 ящиков яблок, массы которых равны соответственно 15, 16, 18, 19, 20 и 31 кг. Две фирмы приобрели 5 ящиков, причём одна из них взяла по массе в 2 раза больше яблок, чем другая. Какой ящик остался в магазине?
Решение: Поскольку одна фирма купила вдвое больше яблок, чем другая, общая масса яблок должна делиться на 3 (тогда 2/3 купит первая компания и ещё 1/3 – вторая). Общая масса всех яблок в магазине равна
15 + 16 + 18 + 19 + 20 + 31 = 119 кг. 1 + 1 + 9 = 11 не  3.
3.
Чтобы получилось число, кратное трём, нужно от 119 отнять 20.
119 – 20 = 99  3. Значит в магазине остался ящик массой 20 кг.
3. Значит в магазине остался ящик массой 20 кг.
Анализ заданий школьного и муниципального этапов всероссийской олимпиады школьников по математике показал, что:
– ежегодно материал «Делимость, свойства и признаки делимости» входит в тематику олимпиады по математике школьного и муниципального этапов;
– задания на делимость, свойства и признаки делимости могут быть включены в варианты олимпиадных заданий для любого класса с 5 по 11;
– олимпиадные задания на делимость, свойства и признаки делимости должны быть различной сложности для того, чтобы, с одной стороны, предоставить практически каждому ее участнику возможность выполнить наиболее простые из них, с другой стороны, достичь одной из основных целей олимпиады – определения наиболее способных ребят в области математики.
Приведём образцы заданий по математике на делимость, свойства и признаки делимости для различных классов, которые встречались на школьном, муниципальном этапах математических олимпиад и могут быть рассмотрены на занятиях математического кружка по решению олимпиадных задач.
Задача 1 (5-6 класс).
Запишите числа 1, 2, 3, 4, 6, 8, 9 в строку так, чтобы из любых двух соседних чисел одно делилось бы на другое.
Ответ: Например: 9, 3, 6, 2, 4, 8, 1.
Задача 2 (5-6 класс).
Придумайте девятизначное число, у которого по крайней мере три разные цифры и которое делится на каждую из них.
Ответ: Например, число 111111124 (делится на 1, на 2 и на 4).
Задача 3 (6-7 класс).
Каждое из двух чисел не делится на 10. Их произведение равно 1000. Чему может равняться их сумма?
Решение: Найдём делители числа 1000. Делителями являются числа: 1, 2, 4, 5, 8, 10, а также числа 125, 200, 250, 500, 1000. Выберем из них два таких делителя, произведение которых равно 1000, а каждый из делителей не делится на 10. Такими делителями являются числа 125 и 8. Найдём их сумму

Ответ: 133.
Задача 4 (6-7 класс)
Записано пятизначное число, делящееся на 9. Кто-то поменял порядок расположения этих цифр. Доказать, что получившееся число делится на 9.
Решение: Из признака делимости на 9 следует, что число делится на 9 тогда и только тогда, когда сумма цифр этого числа делится на 9. Из условия задачи известно, что первое число делится на 9. Значит сумма его цифр делится на 9. Так как от перемены мест слагаемых сумма не меняется, то сумма цифр полученного числа тоже будет делиться на 9, а значит и само число тоже будет делиться на 9.
Задача 5 (7-8 класс). Найти все пятизначные числа вида  (m, n – цифры), которые делятся на 18.
(m, n – цифры), которые делятся на 18.
Решение:  Поэтому число должно делиться на 9 и на 2.
Поэтому число должно делиться на 9 и на 2.
По признаку делимости на 2 получаем, что 
Пусть 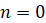 . Тогда число имеет вид
. Тогда число имеет вид  . По признаку делимости на 9 сумма
. По признаку делимости на 9 сумма  должна делиться на 9. Значит m может быть равным только 5. Получили число 51750.
должна делиться на 9. Значит m может быть равным только 5. Получили число 51750.
Пусть  , и число имеет вид
, и число имеет вид  . По признаку делимости на 9 сумма
. По признаку делимости на 9 сумма  должна делиться на 9. Значит m может быть равным только 3 и получается число 51732.
должна делиться на 9. Значит m может быть равным только 3 и получается число 51732.
Рассмотрев остальные варианты, аналогично находим остальные числа: 51714, 51786, 51768. Ответ: 51750, 51732, 51714, 51786, 51768.
Задача 6 (8-9 класс).
Найдите какие-нибудь три последовательных натуральных числа, меньших 1000, произведение которых делится на 9999.
Решение: Например, 99, 100 и 101. Этот пример можно получить, заметив, что  . Ответ: 99, 100 и 101.
. Ответ: 99, 100 и 101.
Задача 7 (8-9 класс).
Сумма цифр натурального числа A равна сумме цифр числа 3A. а) Докажите, что A делится на 3. б) Докажите, что A делится на 9. в) Верно ли, что A обязательно делится на 27?
Решение: а), б) Пусть сумма цифр числа A равна S. Но так как 3A делится на 3, то S делится на 3, тогда и A делится на 3. Отсюда следует, что 3A делится на 9 и S также делится на 9, то есть A делится на 9. в) Не обязательно, можно взять, например, A=9. Ответ. в) Не обязательно.
Опыт использования рассмотренных задач во внеурочной работе на занятиях математического кружка показал, что их решение вызывает большой интерес учащихся, а также способствует развитию математической грамотности школьников, подготовке к участию в олимпиадах разного уровня.
| Количество просмотров: 3449 |


Добавить комментарий