В концепции развития математического образования в РФ поставлен ряд задач, направленных на улучшение качества математической подготовки российских школьников. В ней «…предусмотрено значительное увеличение активных форм работы, направленных на вовлечение учащихся в математическую деятельность, на обеспечение понимания ими математического материала и развития интеллекта, приобретения практических навыков, умений проводить рассуждения, доказательства» [1].

Одной из таких форм работы является привлечение учащихся к проектно-исследовательской деятельности, значимость которой трудно переоценить. Но чтобы использовать исследовательский метод, им нужно владеть. Умения наблюдать, измерять и вычислять, подмечать закономерности, выдвигать гипотезы, проверять их истинность, применяя математический метод, делать выводы, критически осмысливать полученные результаты, применять их в дальнейшем – всё это тот необходимый набор, который востребован для использования данного метода. Возможности внеурочной деятельности (участие в научно-практических конференциях, конкурсах творческих и исследовательских работ) помогают учителю научить школьников элементам исследовательского метода, но в этот процесс вовлечены далеко не все учащиеся. Тогда как требования Федерального государственного образовательного стандарта к результатам освоения обучающимися образовательной программы предусматривают «владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем, способностью и готовностью к самостоятельному поиску методов решения практических задач» [2].

Анализ литературы по данной теме и собственный многолетний опыт работы учителем математики показывает, что для решения этих задач целесообразным становится вовлечение школьников в проектно-исследовательскую деятельность, напрямую связанную с усвоением программного материала.

Такими заданиями, например, можно считать небольшие творческие задачи, которые можно проводить как внутри одного урока, так и предлагать в качестве домашнего задания. Первые навыки такого вида работы начинают прививать ещё в начальной школе, а в 5-6 классах проводить небольшие исследования наиболее благоприятно, учитывая природную любознательность данного возраста. Показать, как математика связана с жизнью, где применяются полученные на уроке знания, можно при выполнении практико-ориентированных задач, которые могут служить как подготовкой к изучению дальнейших тем, так и стимулировать учащихся к самообразованию – необходимому условию исследовательской деятельности.

Приведу несколько примеров так называемых мини-исследований для учащихся разных возрастных групп.

Пример 1: Мини-исследование по определению угла наклона брони танка Т-34, можно проводить при изучении темы «Транспортир» в 5 классе и повторении курса математики 5-6 класса. Оно подготавливает ребят к изучению тем «Углы, образованные двумя параллельными прямыми и секущей» и «Некоторые свойства прямоугольных треугольников», которые будут изучаться в курсе геометрии 7 класса. К тому же данное исследование способствует приобретению первоначального опыта математического моделирования, а в направлении личностного развития играет неоценимую роль в воспитании любви к родине, её истории.

Ход исследования:

Учащиеся просматривают видеоролик «Из воспоминаний командира танка лейтенанта Александра Бурцева» [3], в котором рассказывается о том, что наклонная броня танка являлась предметом гордости танкистов. При толщине брони 45 мм из-за угла наклона снаряду приходилось пробивать толщину в 90 мм (рис.1-2), что давало превосходство нашим танкам перед Пантерами и Тиграми.

Пример 2: Мини-исследование «Космический календарь», проводимое при изучении темы «Масштаб» в 5-6 классе, способствует формированию научной картины мира, правильного мировоззрения, желанию узнать что-то новое.

Ход исследования:

Используя данные современной науки о возрасте Вселенной и её эволюции с момента Большого взрыва до наших дней, учащимся предлагается оценить, сколько лет тому назад произошло то или иное событие. Учитывая, что возраст Вселенной составляет примерно 13,8 млрд лет, будем считать, что один месяц космического календаря ~1млрд. лет, 1 день ~40 млн лет.

Ребята самостоятельно заполняют 3 колонку таблицы, оценивают понятие «время», место и роль человека во Вселенной. В конце исследования можно показать видеоролик из научно-популярного фильма «Космос» [4].

Немаловажную роль в организации обучения и самообразования играют информационные технологии и применение компьютеров. Возможность использования видеоматериалов и интернет-ресурсов способствует усилению визуальной и экспериментальной составляющей. Так в первом примере использовался видеоролик для постановки проблемы, а во втором для подтверждения проведённого исследования.

Пример 3: Мини-исследование «Объём цилиндра» можно проводить как в курсе «Наглядная геометрия» в 6 классе, так и при изучении темы «Объёмы геометрических тел» в старшей школе.

Ход исследования:

Цилиндр заполняется водой, а затем эту воду переливают в прямоугольный параллелепипед. Найдя площадь основания параллелепипеда и измерив его высоту, подсчитывают объём воды. Затем ученикам предлагается найти произведение площади основания цилиндра на его высоту, для чего первоначально производят необходимые измерения, и полученный результат сравнивается с предыдущим. На основании этого выдвигается предположение о том, что объём цилиндра равен произведению площади основания на высоту. Данное предположение доказывается в старшей школе.

Пример 4: Мини-исследование «Площади подобных фигур». Данное исследование, относящееся к теме «Подобие», для учащихся 8 класса можно провести как в классе, так и дома перед доказательством теоремы об отношении площадей подобных фигур.

Ход исследования:

На столе несколько пар подобных фигур, например, пара треугольников или параллелограммов, окружностей. Учитель задаёт вопрос: «Если мы, сделав соответствующие измерения, вычислим площади какой-нибудь пары подобных фигур, найдём их отношение, будет ли оно равно отношению соответствующих линейных размеров?» Ребята высказывают своё предположение. Затем, сделав замеры и вычисления у всех пар подобных фигур, приходят к выводу, что площади подобных фигур относятся как квадрат коэффициента подобия. Очень полезно провести данное исследование и с природным материалом, например, двумя листами одного растения одинаковой формы, но разных размеров (площади листов подсчитываются с помощью палетки). Это задание можно дать на дом.

Пример 5: Известен факт, что любая пирамида имеет чётное число рёбер. К этому выводу можно подвести учащихся, организовав мини-исследование «Конструируем пирамиду» для учащихся старших классов или в курсе «Наглядной геометрии»-5-6 с целью открытия данного математического факта.

Ход исследования:

У учащихся наборы с чётным и нечётным количеством спичек или спиц. Опытным путём ребята пытаются смоделировать из этих спиц пирамиду и приходят к соответствующей гипотезе, которую потом и доказывают.

Многие мини-исследования заинтересовывают ребят и являются первой ступенькой к более глубокому изучению данного вопроса. Приведу пример из собственного опыта работы по подготовке учащихся 10 класса к научно-практической конференции по теме «Развёртки и многогранники».

Если взять равносторонний треугольник, вырезанный из листа бумаги, то без труда из него можно свернуть правильный тетраэдр. Если взять любой другой треугольник или другую фигуру, на которой не обозначены линии сгиба, то всегда ли из неё можно получить многогранник без самопересечений? В процессе опыта с другой развёрткой у учащихся возникают затруднения. Возникает вопрос. Если условием существования треугольника является неравенство треугольника, то какой набор необходимых и достаточных условий должен присутствовать у развёртки, чтобы из неё можно было бы свернуть многогранник? В ходе данного исследования ребята подходят к знакомству с теоремой Александрова о существовании выпуклого многогранника.

В приведенных выше примерах акцент ставился на практическую составляющую учебных исследований, позволяющих школьникам самостоятельно делать открытия неизвестных им ранее фактов. К тому же практико-ориентированные задания способствуют развитию познавательных интересов учащихся, расширению их кругозора, формированию интеграционного мышления, показывая системообразующую роль математики. Огромный опыт по этому вопросу имеет советская и российская педагогическая наука. Всем известны знаменитые труды Я.И. Перельмана, интересные задачи с практическим содержанием И.М. Смирновой и В. А. Смирнова, работы В.А. Далингера [5-7].

Рассмотрим ещё одну функцию учебного исследования – формирование умения анализировать, рассматривать различные способы решения той или иной задачи. Остановимся на примере исследования математических ситуаций, возникающих при доказательствах. Речь идёт обо всех возможных случаях, возникающих при доказательствах теорем. Например, в курсе геометрии 8 класса [8] доказательство теоремы о площади параллелограмма проводится с использованием рисунка.

Исследовательские навыки также хорошо развиваются при решении задач с параметрами. Конечно, решение таких задач занимает немало времени, но среди них есть и те, которые хорошо укладываются в рамки мини-исследований. Например: дан график квадратичной функции   . Изобразите схематически график функции    .

В нашем лицее практикуется индивидуальный вид работы через выполнение тематических типовых расчётов, целью которых является не только обобщение и систематизация материала, но и подготовка к вузовским формам работы. Ниже приведены примеры заданий с параметром из типового расчёта «Уравнения и неравенства» [9], которые можно использовать для проведения мини- исследований аналитического характера.

1. Исследуйте линейное уравнение

2. Исследуйте систему линейных уравнений

3. При каких значениях параметра m, квадратный трёхчлен      можно представить в виде полного квадрата двучлена.

4. Найдите все значения параметра с, при которых неравенство 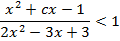  справедливо при всех действительных значениях x.

Как видим из примеров, используя ресурс небольших учебных исследований, можно продуктивно организовать познавательную деятельность учащихся на уроках математики, решая ряд важных дидактических задач.

Итак, какие можно сделать выводы.

Во-первых, даже небольшие исследования – это процесс поисковой познавательной деятельности, направленный на самостоятельное получение новых для учащихся знаний.

Во-вторых, желательно проводить этот вид работы системно, как в процессе изучения программного материала, так и при организации внеурочной работы.

В-третьих, при отборе материала необходимо помнить об основных дидактических функциях учебного исследования (открытия, углубления и систематизации знаний).

Таким образом, небольшие исследования и практико-ориентированные задачи будут способствовать формированию умений и навыков исследовательской деятельности, главной целью которой является всестороннее развитие учащихся.

Используемые источники:

1. Атанасян Л.С., Бутузов В.Ф., Кодомцев С.Б. и др. Геометрия 7-9 кл., М. Просвещение, 2020.

2. Далингер В.А. Методика обучения учащихся доказательству математических предложений. М., Просвещение, 2006.

3. Калашникова А.Г. и др. Типовой расчёт «Уравнения и неравенства» для учащихся 10-11 класса, Новосибирск, изд. НГТУ, 2017.

4. Концепция развития математического образования в РФ, 2014

5. Перельман Я.И. Геометрия на свежем воздухе. М., ООО «Издательство АСТ», 2007.

6. Смирнова И.М., Смирнов В.А. Геометрические задачи с практическим содержанием. М., издательство МЦНМО, 2010

7. Федеральный государственный образовательный стандарт среднего (полного) общего образования. М., Просвещение, 2016.

8. Kosmos. 2014. XviD.HDRip.by.General Film.

9. Интернет-ресурсы: http://www.youtube.com/watch?v=PKojXVULPpE.