Методика формирования универсального умения решать задачи в условиях обновленного ФГОС НОО
Ученики начальных классов сталкиваются с серьёзными трудностями при решении задач. В результатах Всероссийских проверочных работ (ВПР) по математике имеется подтверждение данного факта как на общероссийском уровне, так и в Новосибирской области (более подробно проблема образовательных дефицитов по математике описана автором ранее [2]). В условиях обновленного ФГОС НОО, ФРП по математике, ФОП НОО [7; 8] от учеников требуется умение решать разнообразные задачи: учебные, учебно-познавательные, практические, текстовые, логические и повседневные жизненные ситуации. Самые низкие показатели выполнения всероссийских проверочных работ по математике в 5 классах связаны с заданиями, требующими умения решать задачи. Трудности школьников объясняются нехваткой необходимых навыков, умений и знаний о задаче и процессе решения любых задач, то есть универсального умения решать задачи. Что согласуется с необходимостью формирования универсальных учебных действий (УУД), к которым относится и умение решать задачи не только на уроках математики, но и в других учебных предметах, при формировании функциональной грамотности и, главное, в жизни.
Чтобы решить эту масштабную проблему, необходима современная система работы действующих учителей в методических объединениях. Для руководителей ММО учителей начальных классов нами был разработан и проведен мастер-класс по определению методических решений проблем предметных дефицитов обучающихся на тему «Методика формирования общего умения решения задач». В ходе мастер-класса педагоги подробно проработали универсальные этапы решения задач и выполнили ряд практически работ. В качестве научной основы взята теория Светланы Евгеньевны Царевой: обучение решению текстовых задач, ориентированное на формирование учебной деятельности младших школьников [9].
Сценарий мастер-класса по теме «Методика формирования общего умения решать задачи»
ПЛАН
1 этап – 1. Мотивационно-целевой (Вызов)
2 этап – 2. Операционно-действенный (осмысление)
2.1. Названия этапов и приемов их выполнения.
2.2. Выполнение этапов решения одной и той же задачи.
2.3. Виды заданий для учеников из рабочей тетради «Учимся решать задачи».
3. Рефлексия
До начала мастер-класса:
Руководитель читает статью: Смолеусова Т.В. Этапы, методы и способы решения задачи // Начальная школа. 2003. № 12. С. 62 – 67[4].
Столы подготовлены для работы в четырех группах.
Руководитель раздает подготовленные пакеты с раздаточным материалом в группы.
Подготовлен ватман с таблицей «Этапы решения задач» для заполнения участниками в ходе практической работы.
Для каждой группы подготовлены клей, маркеры, лист А5.
Ход мастер-класса
– Добрый день, коллеги. У наших учеников самый большой дефицит по результатам ВПР по математике – умение решать задачи.
1 этап – мотивация (вызов)
– Для сопоставления между новой и известной информацией об умении решать задачи я предлагаю вам заполнить первую колонку в листе с приемом «До и После» (Приложение № 1.) Индивидуальная работа. (30 сек)
|
До |
Утверждения |
После |
|
|
Существует 5 этапов решения задач |
|
|
|
Чтение задачи – это этап решения задач |
|
|
|
Построение модели – это прием восприятие задачи |
|
|
|
Приём выполнения плана является вторым этапом решения задачи |
|
|
|
Составление и решение обратной задачи является приемом проверки решения задачи |
|
2 этап – операционно-действенный (осмысление)
– Коллеги, сколько этапов решения задач вы знаете? Покажите пальцами (4).
Коллеги, как этапы называются? Каждая команда заполняет «Кластер» (готовая форма для каждой команды, необходимо вписать названия этапов решения задач) (Приложение № 2) (1 мин). (восприятие, поиск плана решения, выполнение плана, проверка).
– Сравним? У кого так, поднимите руки.
Коллеги, приступим к практической части. Каждая команда получает конверт с названиями конкретных приемов выполнения всех этапов решения задачи. Вам необходимо выбрать только те приемы, которые подходят к вашему этапу. Далее одному участнику команды (с помощником) нужно подойти и вклеить в общий лист ватмана соответствующие приемы выполнения этапа решения задачи в соответствующую ячейку (1 группа – 1 этап «Восприятие задачи», 2 группа – 2 этап «Поиск плана решения», 3 группа – 3 этап «Выполнение плана», 4 группа – 4 этап «Проверка»). Группа озвучивает все приемы «своего» этапа решения задачи.
В конверте разрезанные полоски с названиями разных приемов выполнения всех этапов решения задачи (драматизация, разбиение текста на смысловые части, постановка специальных вопросов, построение модели, рассуждения «от условия к вопросу», «от вопроса к условию», составление уравнения, рассуждения по модели, решение уравнений, на модели измерение, счет, логические операции, решение другим способом, подстановка результата в условие, составление и решение обратной задачи) (Практическая работа № 1) (2 мин).
|
|
1 этап |
2 этап |
3 этап |
4 этап |
|
1 группа |
«Восприятие задачи» |
|
|
|
|
2 группа |
|
«Поиск плана решения задачи» |
|
|
|
3 группа |
|
|
«Выполнение плана» |
|
|
4 группа |
|
|
|
«Проверка» |
Презентация результатов практической работы (1 мин)
– Коллеги, для чего вы делали это задание на нашем мастер-классе? Прошу заполнить таблицу № 1 и озвучить.
(Руководитель раздает группам справочные материалы: Смолеусова Т.В. таблица «Этапы и приемы решения задачи» и страницы из пособия Смолеусова Т.В. «Наглядные таблицы по математике для начальных классов»).
– Коллеги, на мастер-классе мы постараемся проработать каждый этап решения задач. Для этого каждая команда получает практическое задание № 2 в соответствии со своим этапом решения задач и в течение 6 минут согласованно его выполняет.
В презентации своей работы, вам необходимо будет ответить на вопрос: для чего вы выполняли это задание? (Практическая работа № 2) (6 мин) У каждой команды ОДНА задача.
I. ВЫПОЛНИТЕ ТОЛЬКО ЭТАП: Восприятие задачи: Участникам представляется текст задачи, к которой необходимо будет составить 2 модели на ватмане (схематический чертеж, чертеж в масштабе), 2 участника представляют текст задачи в виде предметных моделей при помощи пластилина, полосок цветной бумаги, семечек арбуза, тыквы (задачу распечатать). ЗАДАЧУ РЕШАТЬ НЕ НАДО!
II. ВЫПОЛНИТЕ ТОЛЬКО ЭТАП: Поиск плана решения задачи: Участникам нужно «связать» вопрос и условие по словесному заданию отношений. Выполните 3 варианта: «От вопроса», «От условия», составить схемы и таблицы (задачу распечатать) ЗАДАЧУ РЕШАТЬ НЕ НАДО!
III. ВЫПОЛНИТЕ ТОЛЬКО ЭТАП: Выполнение плана решения задачи: Команде необходимо выполнить действия (по плану) разными методами оформить задачу (алгебраическим, арифметическим, смешанным) (задачу распечатать).
IV. ВЫПОЛНИТЕ ТОЛЬКО ЭТАП: Проверка решения задачи: Участникам необходимо проверить решение задачи через 2 приема (решить задачу разными способами, составить обратную задачу и решить ее) (задачу распечатать) ЗАДАЧУ РЕШАТЬ НЕ НАДО!
Презентация результатов практической работы
– Коллеги, выходите к экрану со своими листами с выполненным заданием (моделями, схемами, записями). Встаньте в порядке номеров группы (этапа решения задачи). Озвучьте выполненное задание. Ответьте на вопрос: для чего вы это задание делали на нашем мастер-классе? Прошу заполнить таблицу № 1 (3 мин).
А сейчас рассмотрим методику формирования общего умения решать задачи у младших школьников. В ваших конвертах лежат задания для младших школьников из рабочей тетради Н. Б. Истоминой «Учимся решать задачи» (Практическая работа № 3).
Каждой команде необходимо определить цель задания для учеников (для формирования каких умений) и заполнить таблицу (2 мин).
Практическая работа 3
|
|
Задание из рабочей тетради: Истомина Н.Б. «Учимся решать задачи» |
Цель задания (на формирование какого этапа решения задачи и приема выполнения направлено?) |
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
Презентация результатов практической работы (1 мин)
– Коллеги, прочитайте всем задание для учеников и скажите, для чего это задание вы делали на нашем мастер-классе? Прошу заполнить таблицу № 1.
3 этап – рефлексия
Прием «До и После» завершается.
– Коллеги, вернемся к нашим индивидуальным листам с приемом «До и После» и заполните данную таблицу в третьем столбце «После» (30 сек)
|
До |
Утверждения |
После |
|
|
Существует 5 этапов решения задач |
|
|
|
Чтение задачи – это этап решения задач |
|
|
|
Построение модели – это прием восприятие задачи |
|
|
|
Приём выполнения плана является вторым этапом решения задачи |
|
|
|
Составление и решение обратной задачи является приемом проверки решения задачи |
|
– По каким утверждениям было больше всего несовпадений «до – после» и по какой причине. Как вы думаете? Проверим свои гипотезы?
На экране появляется таблица «До – после» с верным заполнением третьего столбца для сравнения.
В заключение попрошу продолжить два предложения
Раньше я думала, ЧТО ……
А теперь я знаю, ЧТО….. (1 мин).
Желающие (2-3 человека), зачитайте то, что написали.
Как проходил мастер-класс в рамках областного съезда работников образования НСО? Первый вопрос был: сколько универсальных этапов решения любых задач? Покажите количество пальцами.
Практическая работа № 1: Названия этапов и приемов их выполнения
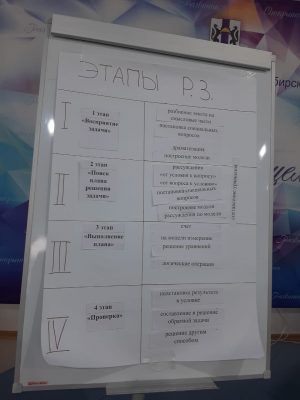
Все поделены на 4 группы. Каждая группа получила конверт с бумажными полосками, на которых напечатаны названия конкретных приемов выполнения всех этапов решения задачи (вперемешку). Необходимо выбрать только те приемы, которые подходят к этапу решения задачи в соответствии с номером группы. Дается время на обсуждение и далее одному участнику команды нужно подойти и вклеить в общий лист ватмана (1 группа – 1 этап «Восприятие задачи», 2 группа – 2 этап «Поиск плана решения», 3 группа – 3 этап «Выполнение плана», 4 группа – 4 этап «Проверка»). Руководители ММО учителей начальных классов Новосибирской области включились в совместную работу.
Выходили к единому ватману и вклеивали в соответствующую ячейку результаты обсуждения в своей группе.
Результатом работы всех групп явилась единая таблица с наклеенными названиями этапов и приемов выполнения всех четырех универсальных этапов решения любой задачи.
Практическая работа № 2: Выполнение этапов решения одной и той же задачи
Каждая команда педагогов получила текст ОДНОЙ И ТОЙ ЖЕ ЗАДАЧИ и выполняли задание в соответствии со своим этапом решения задач.
I. Восприятие задачи: участникb к тексту задачи составляли 2 модели на ватмане (схематический чертеж, чертеж в масштабе) и в виде предметных моделей при помощи пластилина, полосок цветной бумаги, семян арбуза, тыквы.
II. Поиск плана решения задачи: участники «связывали» вопрос и условие по словесному заданию отношений «От вопроса», «От условия», составляли схемы и таблицы.
III. Выполнение плана решения задачи: педагоги разными методами оформляли задачу (алгебраическим, арифметическим, смешанным).
IV. Проверка решения задачи: педагоги решали задачу разными способами и записывали по действиям с вопросами и по действиям с пояснениями.
Представители групп презентовали работу группы.
Практическая работа № 3: Виды заданий для учеников из рабочей тетради «Учимся решать задачи»
Педагогам были предложены задания для младших школьников из рабочей тетради Н. Б. Истоминой «Учимся решать задачи» для подробного рассмотрения методики формирования общего умения решать задачи и определения методической цели заданий.
В презентации каждой практической работы педагоги отвечали на вопрос: ДЛЯ ЧЕГО ЭТО ЗАДАНИЕ?
В результате обсуждения видов заданий из учебного материала и анализа методики формирования общего умения решать задачи педагоги пришли к выводу о необходимости системного подхода к обучению и развитию данного навыка у учеников. Они подчеркнули важность пошаговой работы над формированием каждого составного умения решать задачи и регулярного практического применения новых знаний и навыков в различных контекстах на уроках и во внеурочных занятиях. Например, в курсе по функциональной грамотности, на занятиях подготовки к олимпиадам или регулярное включение подобных заданий в уроки математики.
Мастер-класс стал не только площадкой для изучения методики формирования общего умения решать задачи, но и возможностью для каждого участника самостоятельно оценить свои результаты и планы на будущее, а также стимулировал каждого участника к самоанализу и постановке новых целей для дальнейшего саморазвития и совершенствования.
Список литературы
1. Истомина Н.Б. Истомина Н.Б. Учимся решать задачи. М.: Бином. Лаборатория знаний. 2022.
2. Смолеусова Т.В. Трудные темы в обучении младших школьников математике: методические рекомендации на основе анализа результатов ВПР // Интерактивное образование. 2023. №108-109. https://io.nios.ru/articles2/126/36/trudnye-temy-v-obuchenii-mladshih-shkolnikov-matematike-metodicheskie-rekomendacii
3. Смолеусова Т.В. Таблица: Этапы и приемы решения задачи. https://vk.com/doc512007464_478955574?hash=zFwTjDSZfxhuFc8VLDps9NaM9ZHVLZpGhi02EZGtM2P&dl=nQUx7QfGifHK6nEGzTFMwHGFGXTLyfaJrCbgPK6wLpk
4. Смолеусова Т.В. Этапы, методы и способы решения задачи // Начальная школа. 2003. № 12. С. 62-67. https://vk.com/doc512007464_478952087?hash=9sYuzAzIJ0EhRVMM8ibRX6ZUBxcbincMpjvjc4y6fRk&dl=TRlBuXmj7ZKGAjW8MTw04aVhQvobFc3PVy7Yyk3RoCg
5. Смолеусова Т.В. Урок математики во 2 классе «Моделирование текстовых задач»: методические рекомендации// Интерактивное образование. 2024.№ 111. https://vk.com/doc512007464_592118953?hash=oZlZR15u7rXkE1Pzs5kW3KKp0HWbj...
7. Федеральная рабочая программа по математике. 2023 г. https://edsoo.ru/rabochie-programmy/
8. Федеральный государственный образовательный стандарт начального общего образования. 2021 г. https://edsoo.ru/normativnye-dokumenty/
9. Царева С.Е. Обучение решению текстовых задач, ориентированное на формирование учебной деятельности младших школьников. Новосибирск: Изд-во НГПУ. 1998. 136 с. https://repo.nspu.ru/bitstream/nspu/976/1/obuchenie-resheniyu-tekstovyh-za.pdf
| Количество просмотров: 1747 |
















Добавить комментарий